Assigned Reading on the Syntax of Expressions

This work is to be done before Exam 1.

Read Sections 2.1 and 2.2 on pp. 28 – 33 of Sethi (up to and including the figure at the top of p. 33).

A. Problems from Sethi

Do problems 2.1, 2.2, 2.3, 2.7, and 2.8 on pp. 49 – 50 of Sethi.

Problem 2.1:

Rewrite the following expressions in prefix notation. Treat sqrt as an operator with one argument.

Problem 2.2:

Rewrite the expressions of Exercise 2.1 in postfix notation

Solution
(a) a b * c +
(b) a b c + *
(c) a b * c d * +
(d) a b c + * d *
(e) b 2 / b 2 / b 2 / * a c * - SQRT + a /

Problem 2.3:

Draw abstract syntax trees for the expressions in Exercise 2.1

Solution

(a) Abstract Syntax Tree:

ExprTree plus + star * plus--star c c plus--c a a star--a b b star--b

(b) Abstract Syntax Tree:

ExprTree star * a a star--a plus + star--plus b b plus--b c c plus--c

(c) Abstract Syntax Tree:

ExprTree plus + star1 * plus--star1 star2 * plus--star2 a a star1--a b b star1--b c c star2--c d d star2--d

(d) Abstract Syntax Tree:

ExprTree star1 * star2 * star1--star2 d d star1--d a a star2--a plus + star2--plus b b plus--b c c plus--c

(e) Abstract Syntax Tree:

ExprTree div1 / plus + div1--plus a1 a div1--a1 div2 / plus--div2 sqrt sqrt plus--sqrt b1 b div2--b1 num2_1 2 div2--num2_1 minus - sqrt--minus star1 * minus--star1 star2 * minus--star2 div3 / star1--div3 div4 / star1--div4 a2 a star2--a2 c c star2--c b2 b div3--b2 num2_2 2 div3--num2_2 b3 b div4--b3 num2_3 2 div4--num2_3

Problem 2.7:

Draw abstract syntax trees for the expressions in Exercise 2.6 (listed below):

Solution

(a,b) Abstract Syntax Tree:

ExprTree plus + num2 2 plus--num2 num3 3 plus--num3

(c,e) Abstract Syntax Tree:

ExprTree plus + num2 2 plus--num2 star * plus--star num3 3 star--num3 num5 5 star--num5

(d) Abstract Syntax Tree:

ExprTree star * plus + star--plus num5 5 star--num5 num2 2 plus--num2 num3 3 plus--num3

Problem 2.8:

Postfix expressions can be evaluated with the help of the stack data structure, as follows:

  1. Scan the postfix notation from left to right.
    • a. On seeing a constant, push it onto the stack.
    • b. On seeing a binary operator, pop two values from the top of the stack, apply the operator to the values, and push the result back onto the stack.
  2. After the entire postfix notation is scanned, the value of the expression is on top of the stack.

Illustrate the use of a stack to evaluate the expression 7 7 * 4 2 * 3 * −.

Solution

Stack evaluation of 7 7 * 4 2 * 3 * -:

Stack           Remaining Input
─────────────   ──────────────────
                7 7 * 4 2 * 3 * -
7               7 * 4 2 * 3 * -
7 7             * 4 2 * 3 * -
49              4 2 * 3 * -
49 4            2 * 3 * -
49 4 2          * 3 * -
49 8            3 * -
49 8 3          * -
49 24           -
25

B. Infix, Prefix, and Postfix Syntax Exercises

Problem 1: Operator Precedence and Abstract Syntax Trees

In a certain language expressions are written in infix syntax. The language has binary, prefix, and postfix operators that belong to the following precedence classes:

Precedence ClassSymbolBinary OpsPrefix OpsPostfix OpsAssociativity
1st Class (highest)#~~[none]right
2nd Class@[none][none]$left
3rd Class (lowest)%^@[none]right

Problem 1(a): Say which operator is applied last in the following expression, and then draw the abstract syntax tree of the expression. [To help you, subscripts have been attached to each operator to indicate its precedence class and whether that class is left- or right-associative, even though this information can also be obtained from the above table.]

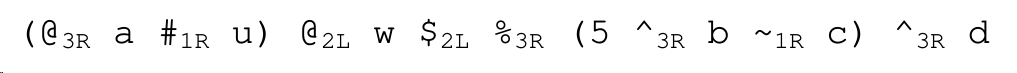
alt text

Solution

The operator % is applied last.

ExprTree n_pct % n_dol $ n_pct--n_dol n_xor1 ^ n_pct--n_xor1 n_at1 @ n_dol--n_at1 n_at2 @ n_at1--n_at2 n_w w n_at1--n_w n_hash # n_at2--n_hash n_a a n_hash--n_a n_u u n_hash--n_u n_xor2 ^ n_xor1--n_xor2 n_d d n_xor1--n_d n_5 5 n_xor2--n_5 n_til ~ n_xor2--n_til n_b b n_til--n_b n_c c n_til--n_c

Problem 1(b): Rewrite the expression in prefix syntax.

Solution
% $ @ @ # a u w ^ ^ 5 ~ b c d

Problem 1(c): Rewrite the expression in postfix syntax.

Solution
a u # @ w @ $ 5 b c ~ ^ d ^ %

Problem 2: Postfix to Prefix Conversion

Draw the AST of the following postfix syntax expression, and rewrite the expression in prefix syntax. A subscript has been attached to each operator that shows the operator’s arity. [The operators in this question and the next are not related to the operators in question 1.]

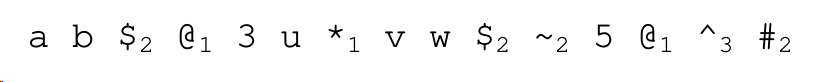
alt text

Solution
ExprTree n_hash # n_at1 @ n_hash--n_at1 n_caret ^ n_hash--n_caret n_dol1 $ n_at1--n_dol1 n_a a n_dol1--n_a n_b b n_dol1--n_b n_3 3 n_caret--n_3 n_tilde ~ n_caret--n_tilde n_at2 @ n_caret--n_at2 n_star * n_tilde--n_star n_dol2 $ n_tilde--n_dol2 n_u u n_star--n_u n_v v n_dol2--n_v n_w w n_dol2--n_w n_5 5 n_at2--n_5

Prefix syntax:

# @ $ a b ^ 3 ~ * u $ v w @ 5

Problem 3: Prefix to Postfix Conversion

Draw the AST of the following prefix syntax expression, and rewrite the expression in postfix syntax. A subscript has been attached to each operator that shows the operator’s arity.

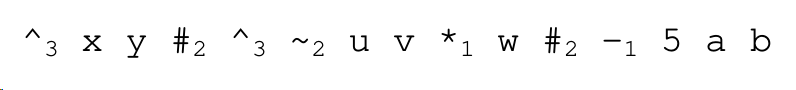
alt text

Solution
ExprTree n_caret0 ^ n_x x n_caret0--n_x n_y y n_caret0--n_y n_hash0 # n_caret0--n_hash0 n_caret1 ^ n_hash0--n_caret1 n_b b n_hash0--n_b n_tilde ~ n_caret1--n_tilde n_star * n_caret1--n_star n_hash1 # n_caret1--n_hash1 n_u u n_tilde--n_u n_v v n_tilde--n_v n_w w n_star--n_w n_minus - n_hash1--n_minus n_a a n_hash1--n_a n_5 5 n_minus--n_5

Postfix syntax:

x y u v ~ w * 5 a # ^ b # ^